Sampling

The first step to performing Fourier transforms on computers is sampling. Say you have an analog signal whose Fourier transform you’d like to compute. This signal could be the response of a certain circuit that you built in the lab. It could be the signal that a radio antenna is measuring at a certain FM frequency. It could also be the signal that a radio telescope is recording of outer space. To compute the Fourier transform of any of these signals, you need to first digitize the analog signal.

In most electronic circuits, the digitization is performed by a ADC or an analog-to-digitial convertor. The ADC polls the analog signal at a specified interval and records what the value of the analog function is at that point. This is called sampling. In this section we will discuss what the interval of sampling (or sampling frequency) should be for any analog function.

Let’s try to sample this sine-wave:

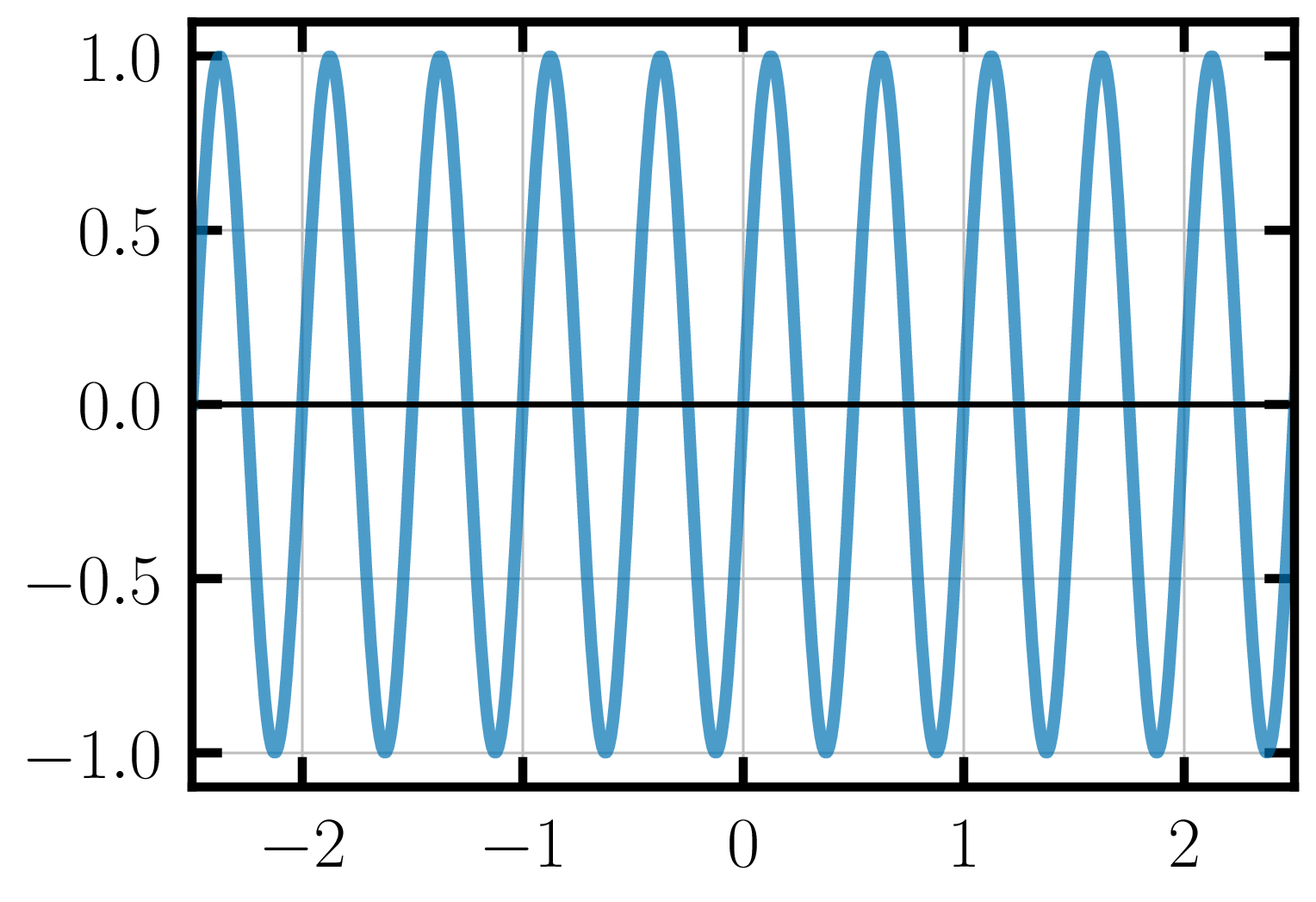
If we have sampled this function the right number of times, we should be able to reconstruct the function by connecting all the points that have been sampled. Let us try a few different sampling frequencies.

The period of this sine-wave is 2 Hz so let’s try sampling this function at 2 Hz.

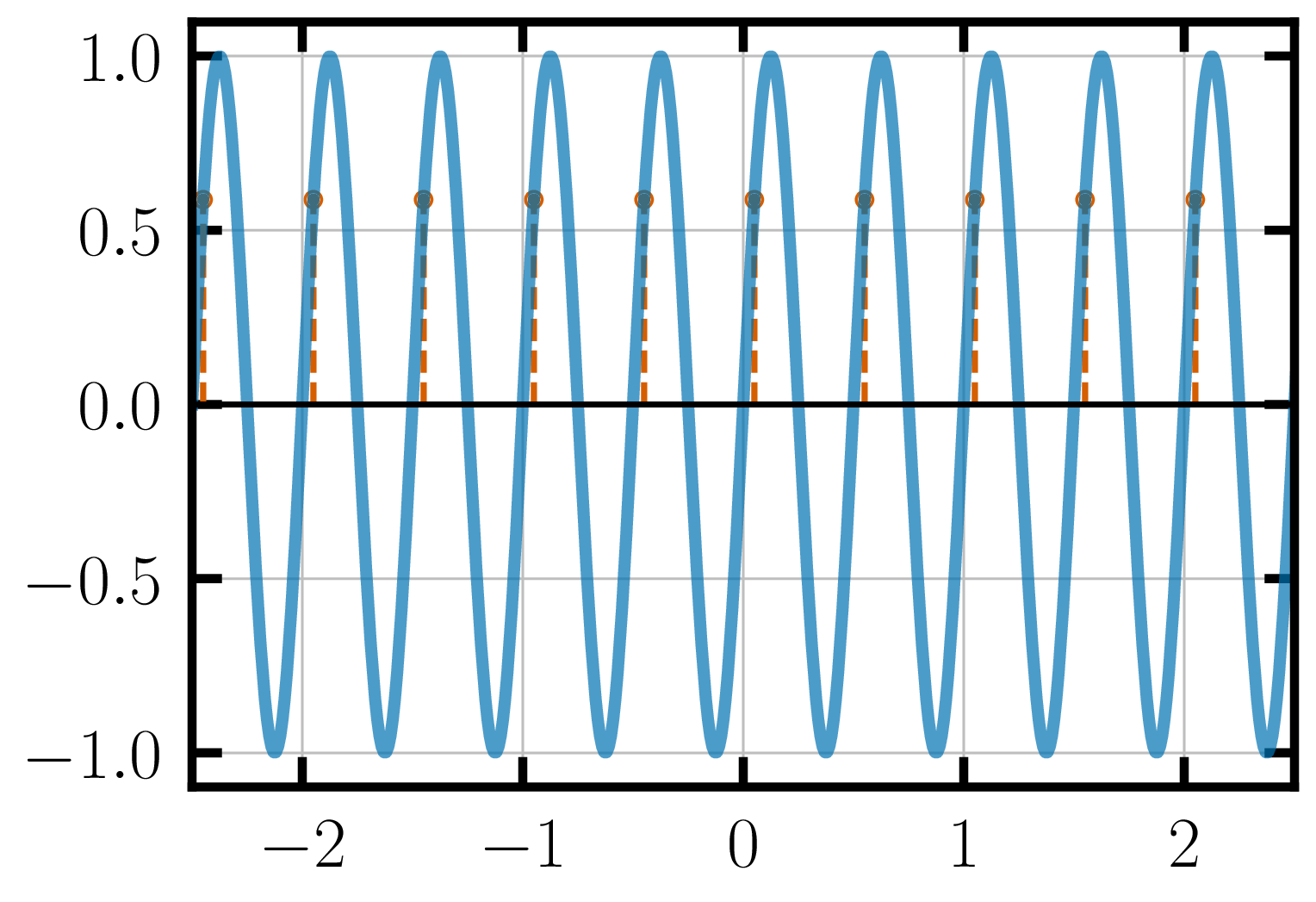
Sine Wave Undersamping — $\nu_0=2\text{ Hz}, \quad f_s = 2\text{ Hz}$

The value $\nu_0$ shows the frequency of the sine wave we are trying to sample and the value of $f_s$ is the sampling frequency we are currently using. If we connect the points that we have sampled using $f_s = 2$ Hz, we get a straight line instead of the sine-wave that we are trying to recreate. Clearly, sampling at the frequency of the signal is not sufficient. Let us try sampling at twice the frequency of the signal.

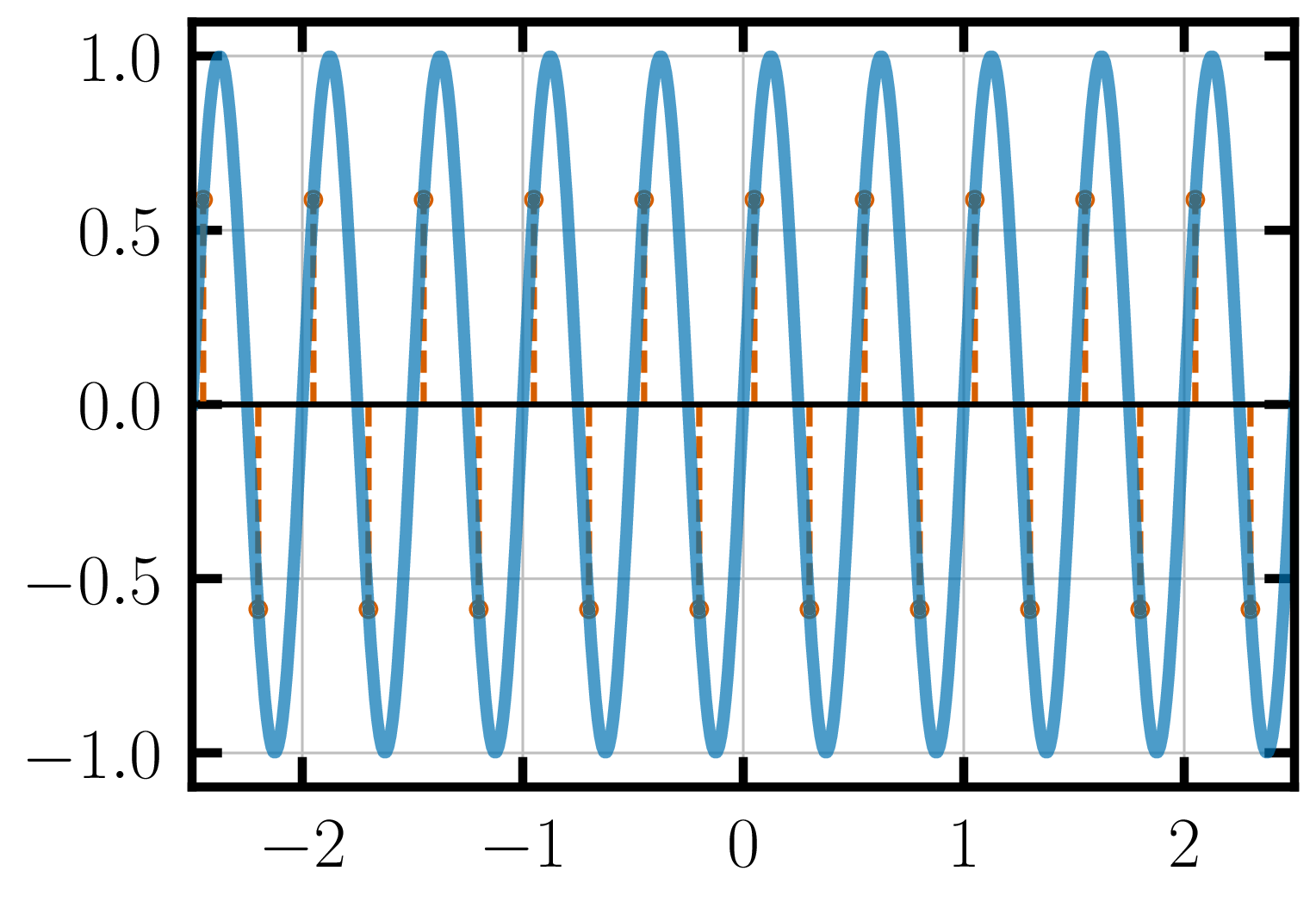
Sine Wave Nyquist — $\nu_0=2\text{ Hz}, \quad f_s = 4\text{ Hz}$

At this frequency, it is evident that the signal we are trying to reconstruct is sinusoidal in nature. However, using these points we would infer the wrong amplitude of the signal. Moreover, it is still unclear if the signal is a sine-wave or a saw-tooth type function. If we knew apriori that the signal we are trying to construct is a sine wave and if by chance our sampling points lay on the peak amplitude of the signal, we would have been able to reconstruct the sine wave we wanted. Let’s turn up the sampling frequency a little bit more:

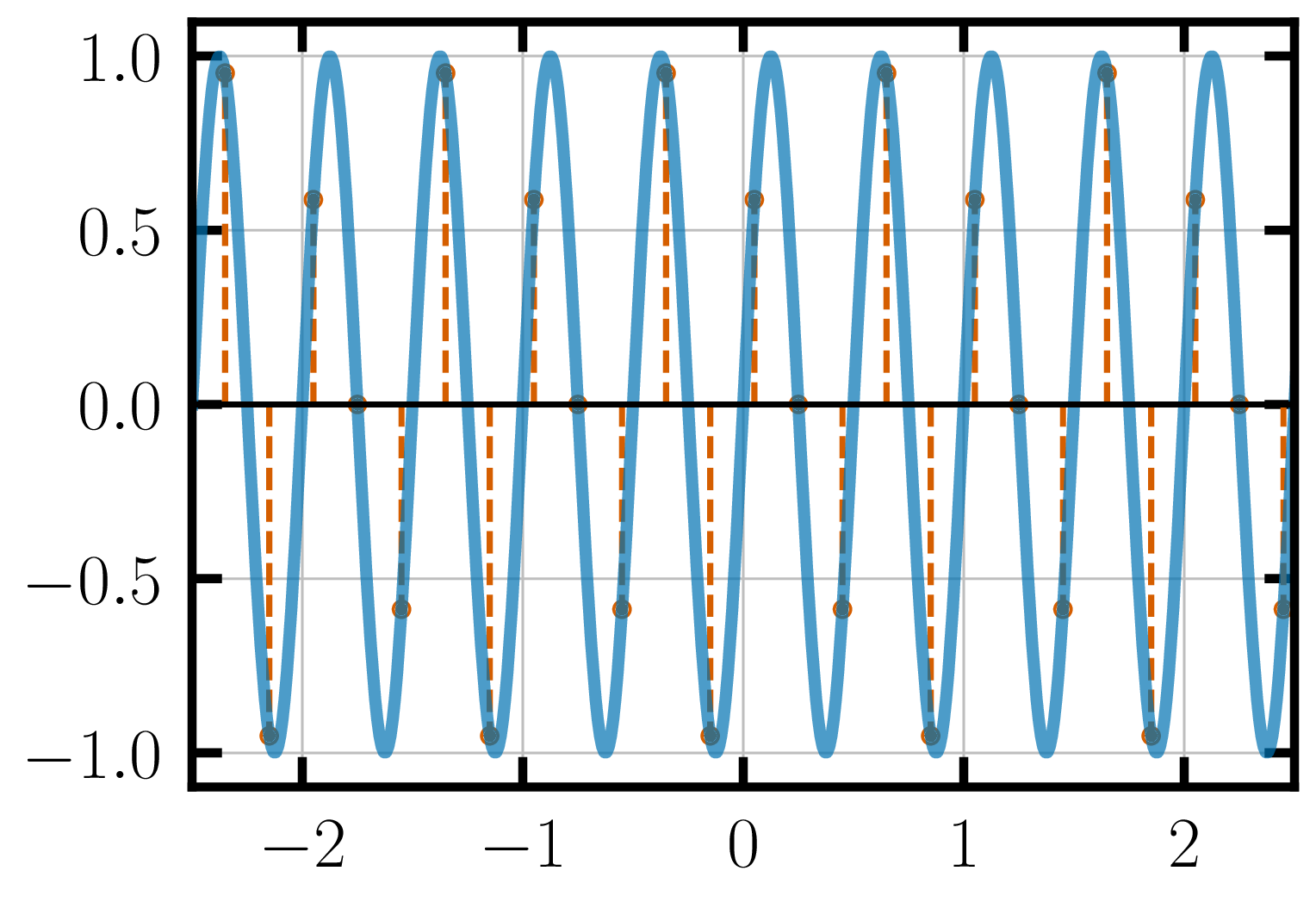
Sine Wave Oversampling — $\nu_0=2\text{ Hz}, \quad f_s = 5\text{ Hz}$

When the sampling frequency is greater than twice the frequency of the signal we are trying to sample, the sampled points recreate the original signal without any loss of information. That is, when digitizing analog signals, the ADC should operate at twice the maximum frequency of the input analog to “completely capture” it. This was first discovered by Vladimir Kotelnikov in 1933 and then independently by Harry Nyquist, Claude Shannon, E.T. Whittaker and others later on. You might sometimes hear it being referred to as “Nyquist-Shannon” sampling theorem.

If an analog signal is sampled at exactly twice the maximum frequency, it is said to be Nyquist-sampled. If the sampling frequency is lower, it is an under-sampled signal and if the sampling frequency is higher, it is an over-sampled signal.

Sampling Theorem

$\begin{equation*} \boxed{ f_s \geq 2f_{max} } \end{equation*}$

The sampling frequency should be twice the maximum frequency of the input analog signal. Say we are trying to sample the analog signal shown below:

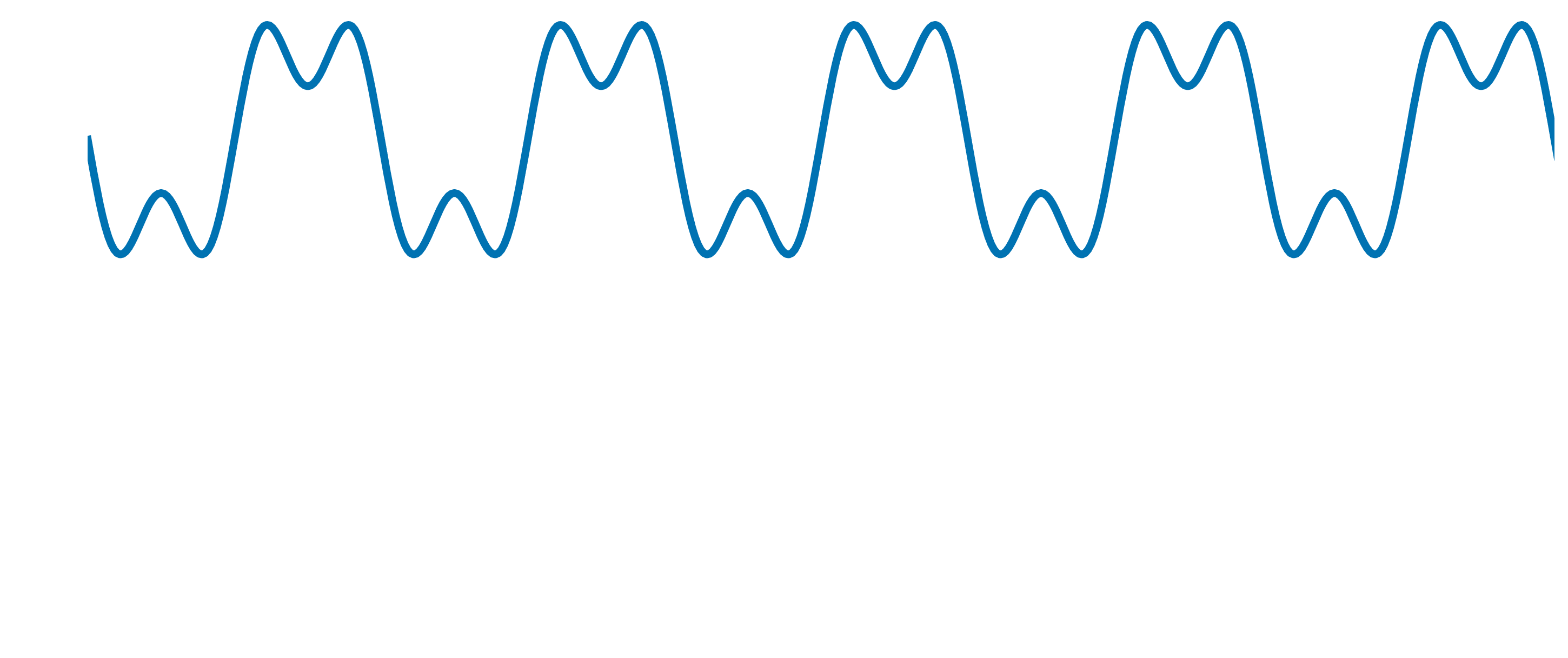
Sum of two sines — $f(t) = 2\sin(3\omega_0 t) + \sin(\omega_0 t), \quad \nu_0 = 1\text{ Hz}$

The signal consists of two different sine waves- one with a frequency of 3 Hz and the other with a frequency of 1 Hz.

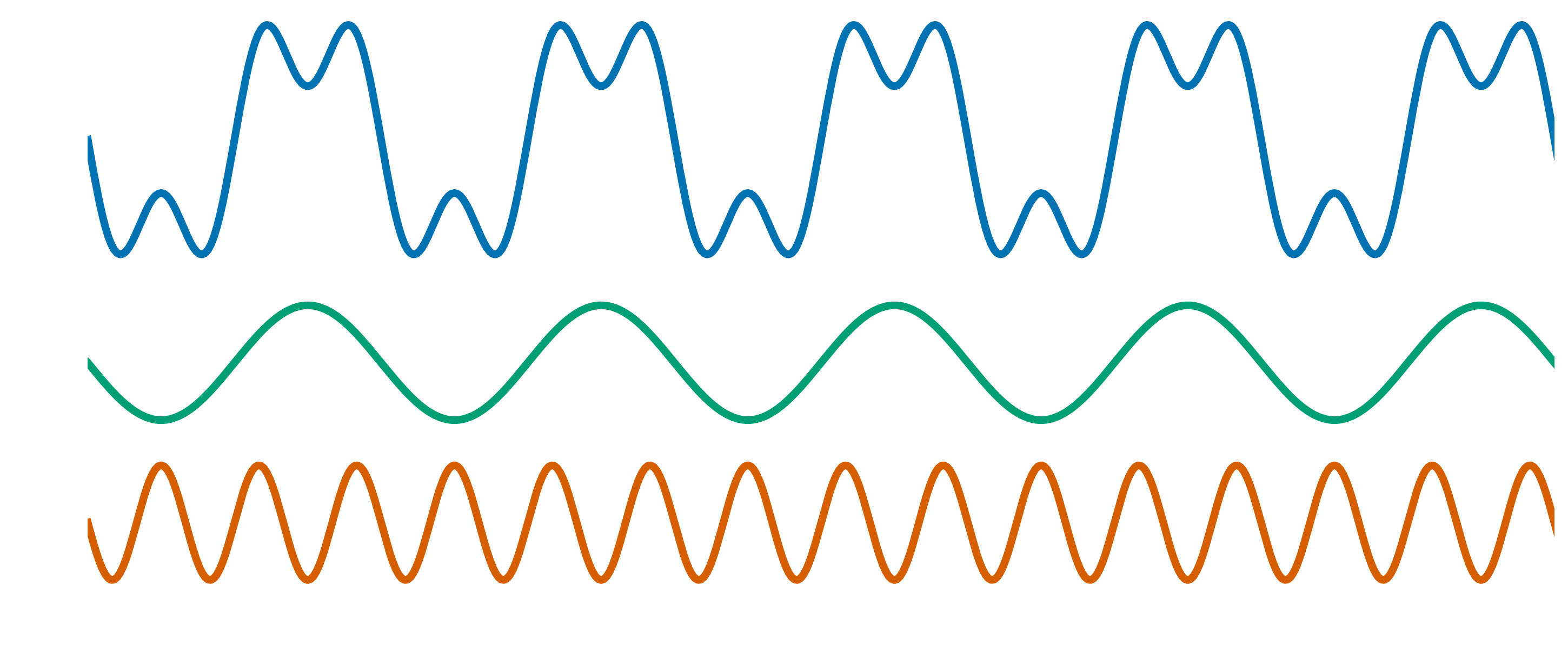
Sum of sines — $f(t) = 2\sin(3\omega_0 t) + \sin(\omega_0 t), \quad \nu_0 = 1\text{ Hz}$

What do you think should be the sampling frequency for this signal?

Deepthi Gorthi Radio astronomer

Sampling

Sampling Theorem